デジタル信号の高調波とは【ノイズ対策】

ノイズ試験におけるEMI(エミッション)で問題になることがあるデジタル回路の高調波の解説です。

の3つに分けて解説します。この記事は「矩形波の周波数成分と包絡線」です。

デジタル信号とノイズ

デジタル回路は、電圧によって信号の”0″と”1″を表現し、伝送しています。

一般的には、デジタル信号は次の図のような波形となっていて、矩形波と呼ばれます。

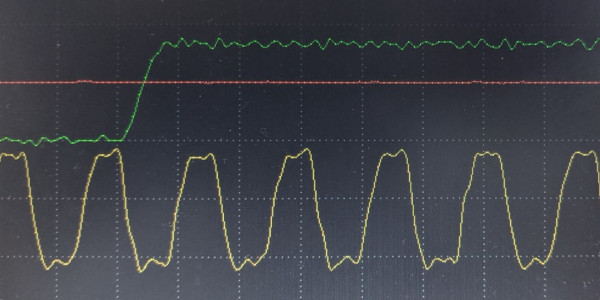
この図で、上の緑色の波形がデータ信号、下の黄色の波形がクロックです。クロックは常に”0″と”1″を繰り返しています。クロック信号は電圧変化の回数が非常に多いため、EMIへの影響も大きくなります。

等間隔の周波数でノイズが出ている場合は、高調波対策をすることでレベルを下げられる可能性があります。

矩形波の周波数成分

矩形波に限りませんが、信号波形(定義が難しい)は正弦波の重ね合わせでできています。

数式で確認

矩形波をフーリエ級数展開すると数式内で高調波を確認できます。

矩形波の式を展開すると次のようになります。(デューティ比が50%のとき)

\[f(x) = \frac{4}{\pi}\{\sin(x) + \frac{1}{3}\sin(3x) + \frac{1}{5}\sin(5x) + \frac{1}{7}\sin(7x) + …\}\]

各sinの項の振幅と周波数に注目すると、

1つ目：基本波。周波数は1、振幅も1
2つ目：周波数は3倍、振幅が1/3 (3倍波)
3つ目：周波数は5倍、振幅が1/5 (5倍波)
4つ目：周波数は7倍、振幅が1/7 (7倍波)

シミュレーションFFTで確認

LTspice上で矩形波を発生させて、FFTで周波数成分を確認します。

LTspiceのシミュレーション方法は別の記事で書きます。ファイルは先にGitHubにアップしました。

次の条件の矩形波を発生させて、その電圧波形をFFTしました。

振幅: 1 V
周波数: 10 MHz
デューティ比: 50%
立ち上がり・立ち下がり時間: 15 ns

10 MHz, 30 MHz, 50 MHz, ・・・と、10 MHz の奇数倍の周波数にスペクトラムが立っています。縦

軸の単位はデシベル(dB)なのでわかりにくいですが、順に1/3, 1/5, ・・・となっています。具体的な数値は下の表のようになっていて、展開した数式どおりの分布となっています。

周波数 (MHz)	フーリエ成分	正規化フーリエ成分
10	0.6366	1.000
30	0.2122	0.3333
50	0.1273	0.2000
70	0.09095	0.1429

クロック(矩形波)の高調波

高調波の特徴

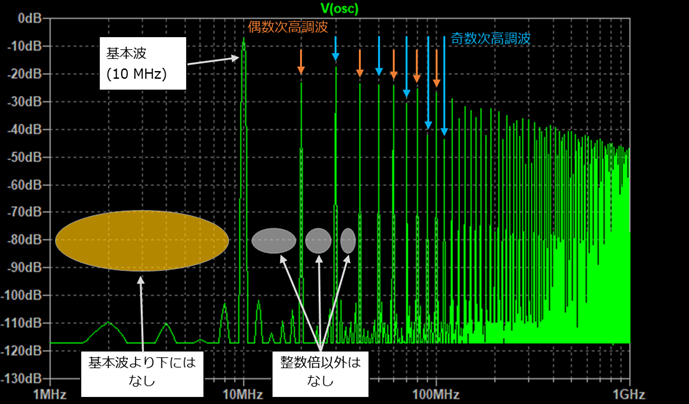
高調波には次のような性質があります。

スペクトルの間隔は基本波の周波数と同じ
基本波よりも低い周波数に成分は存在しない
基本波と高調波、隣接する高調波との間には成分は存在しない
N倍波のレベル(振幅)は基本波の1/N (Nは奇数)
デューティ比が50%の場合は偶数次の高調波は存在しない

クロック波形の周波数成分

クロックの波形を形成する成分のうち、支配的なものは基本波と次数の低い高調波です。

次の図に示す基本波に、3, 5, 7, 9次高調波を順に加算して、合成波形を確認してみます。

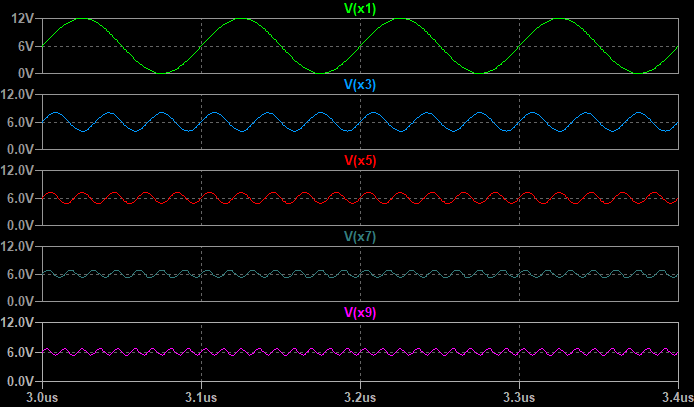
基本波に、奇数次の高調波を順に加えていくと以下のような波形になります。

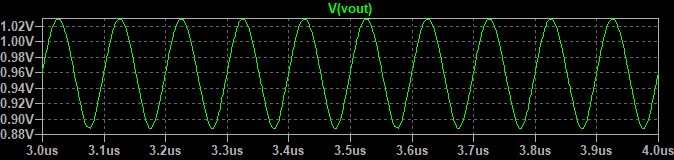
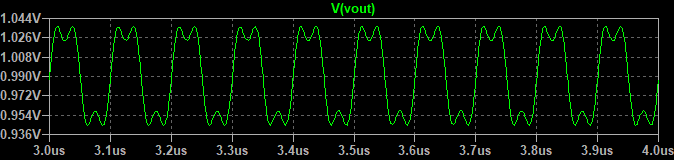
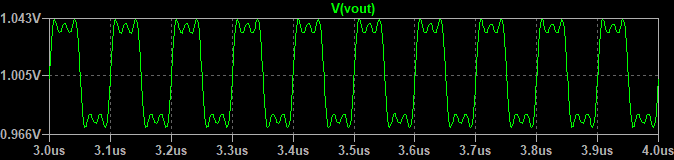
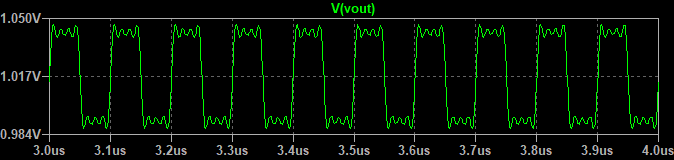
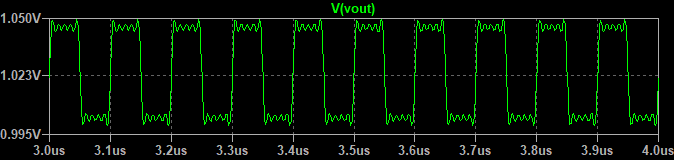
主観ではありますが、基本波と3次高調波を足し合わせた時点で矩形波に近い波形となっています。加える波の次数が5次、7次、9次と高くなると、加算したときの波形の変化は小さくなります。(高次の高調波は振幅が小さいため。)

逆に考えると、高い次数の高調波はクロック波形にあまり影響を与えません。そのため、ローパスフィルタ(LPF)を使って高周波部分を除去すると、波形を大きく変えずに高周波ノイズを抑えることができます。もちろん、対象の機器やデバイスが正常動作する範囲でフィルタをかける必要があります。

LPFを追加してシミュレーション

LTspice上で、LPFを追加して周波数成分を確認しました。フィルタの定数はシミュレーション波形を見ながらカットアンドトライで決めています。

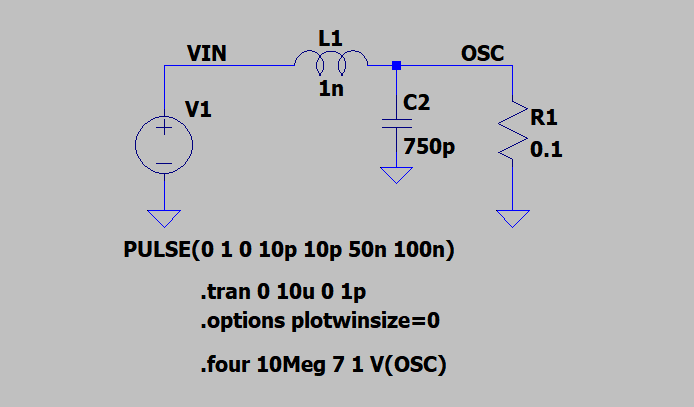
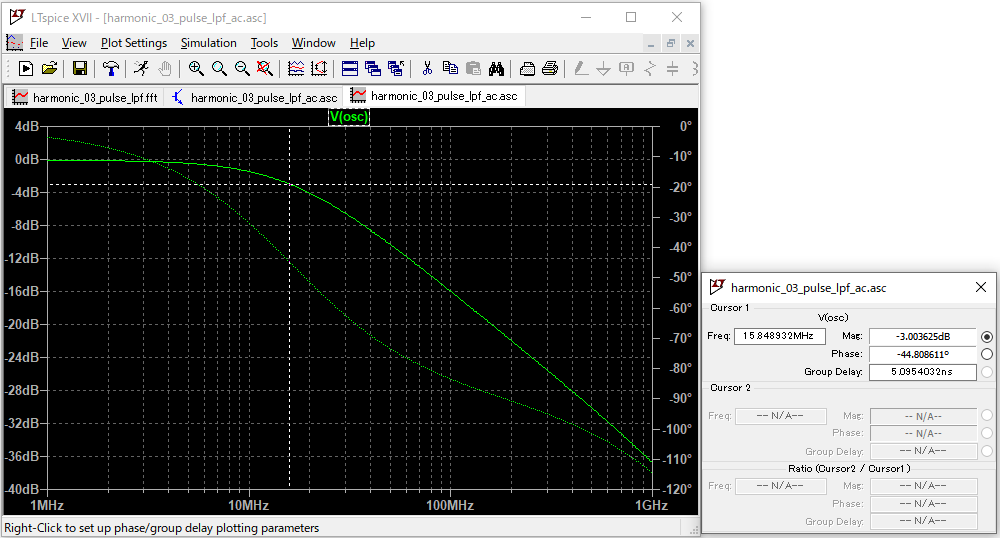
まず、このフィルタの周波数特性です。15.8 MHz付近がカットオフ周波数になっています。(クリックで拡大)

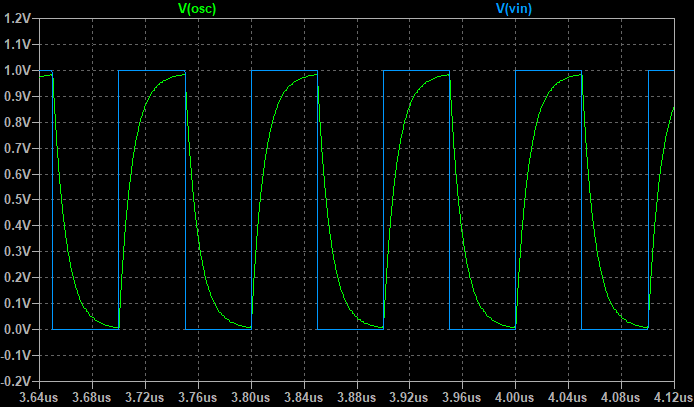
下図は時間軸での波形で、青色はフィルタを通る、緑色はフィルタ通過後です。フィルタを通過することで高周波成分が除去され、波形がなまっています。波形はなまっていますが、クロックとしては問題なく動くと考えられます。(経験上。この波形で良いかどうかはケースバイケース。)

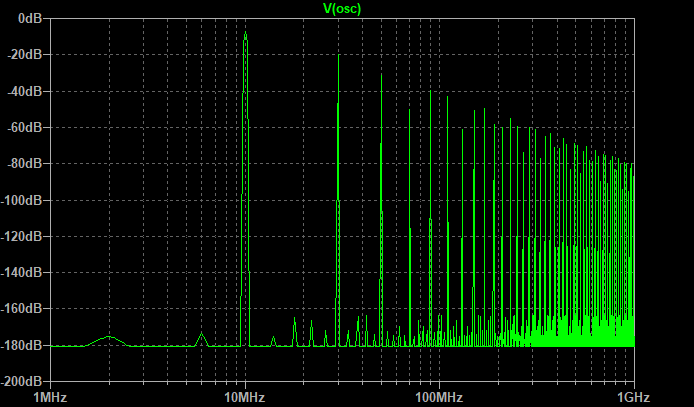
FFTで周波数成分を確認すると、下図のようにフィルタ通過後は高周波成分が減衰しています。(緑：フィルタ通過前、青：フィルタ通過後。さっきと色が逆です。)

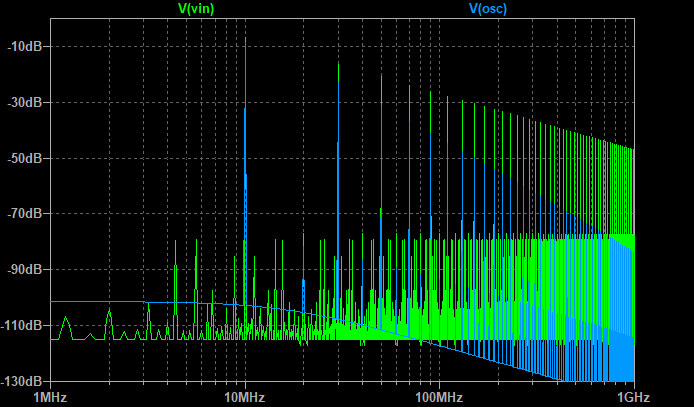
クロック波形を大きく崩すことなく、70 MHzから1 GHzにかけての高調波を減衰できているので、ノイズ対策として効果があると考えられます。

クロック波形と周波数成分の関係

図のような台形波を考えます。
(現実のクロック波形は台形波です。立ち上がり(立ち下がり)時間が0ではないため。)

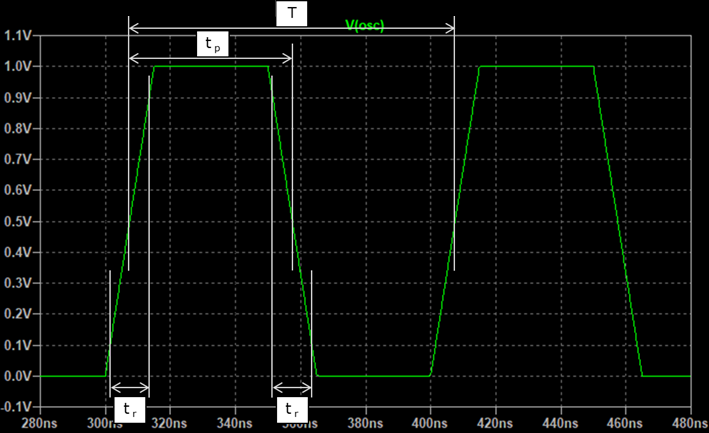
周期：T
パルス幅：t_p
立ち上がり時間：t_r
立ち下がり時間：t_r (立ち上がり時間と同じ)
デューティ比：50%

立ち上がり成分のカットオフ周波数

立ち上がり時間と、周波数成分のカットオフ周波数(振幅が-3 dBとなる周波数)f_rの関係は、次の式が知られています。

\[f_r = \frac{0.35}{t_r}\]

立ち上がり時間が1 nsの場合、過渡オフ周波数は350 MHzとなります。

高調波の包絡線

この矩形波のスペクトラムの包絡線を考えます。(厳密ではなく簡易的に)

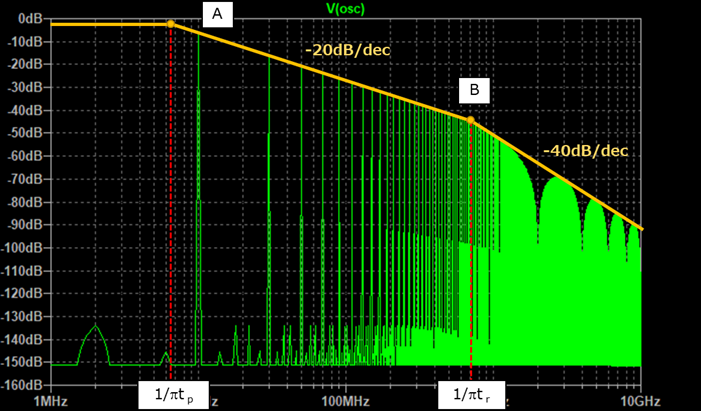
LTspiceのFFT結果に、直線で包絡線を追記しました。図中の縦軸・横軸の値はここでは無視して読み進めてください。

A点とB点の2箇所で直線の傾きが変わります。各点間の領域では、次のようにレベルが変化します。

A点よりも低い周波数では、包絡線のレベルは一定
A点とB点の間では、-20dB/decで減少
B点よりも高い周波数では、－40dB/decで減衰

境界の周波数とノイズ対策

各点の周波数はそれぞれパルス幅と立ち上がり時間で決まります。

A点の周波数はパルス幅t_pで決まる：\(f_A = 1/(\pi t_p)\)
B点の周波数は立ち上がり時間t_rで決まる：\(f_B=1/(\pi t_r)\)

つまり、A点とB点の位置は、波形を調整することで次のように動かすことができます。

パルス幅が小さくなると(周波数が高くなると)、A点が右に移動する
立ち上がり(立ち下がり)が急峻になると、B点が右に移動する

一般的なノイズ対策の

クロックの周波数を下げる
立ち上がり(立ち下がり)速度を下げる(波形をなまらせる)

が有効な手法であることと合致します。クロック周波数を下げてA点を左に動かしたり、立ち上がり速度を緩やかにすることでB点を左に動かすことで、高調波のレベルが下がるからです。

まとめ

高調波の特徴

スペクトルの間隔は基本波の周波数と同じ
基本波よりも低い周波数に成分は存在しない
基本波と高調波、隣接する高調波との間には成分は存在しない
N倍波のレベル(振幅)は基本波の1/N (Nは奇数)
デューティ比が50%の場合は偶数次の高調波は存在しない
矩形波の形状は低い次数の高調波成分が支配的

ノイズ対策

次の方法で高調波に起因するノイズレベルを下げることができます。

ローパスフィルタで高次の高調波を除去する
クロック周波数を下げる
立ち上がり(立ち下がり)速度を下げる

デジタル信号の高調波とは【ノイズ対策】

デジタル信号とノイズ