目次
- 1. LED (発光ダイオード)
- 2. 電流制限
-
- 2-1. LEDの電流について
- 2-2. LEDに流せる最大電流
- 2-3. VF (順方向電圧降下)
- 2-4. 逆耐圧
- 3. 制限抵抗 (電流制限抵抗)と計算方法
-
- 3-1. 電流制限抵抗
- 3-2. 計算に使う法則
- 3-2-1. オームの法則
- 3-2-2. キルヒホッフの第一法則 (電流則)
- 3-2-3. キルヒホッフの第二法則 (電圧則)
- 3-3. 計算まとめ
- 4. 計算例
- 5. シミュレーションで確認
- 5. LEDが複数個あるとき
LED (発光ダイオード)
LED(=Light Emitting Diode、発光ダイオード)はダイオードの一種で、ほかのダイオードと同じように一方向にだけ電流が流れます。電流が流れる方向が順方向です。
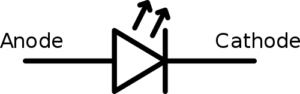
これはLEDの回路図記号で、アノード(Anode)からカソード(Cathode)の方向へ電流が流れます(回路記号の三角形の向きに電流が流れると覚えればOK)。
砲弾型LEDの場合は、長い方の足がアノードです。なので、長い方を電源の+に近いほうにつなぎます。
(回路図記号・・・正確には電気用図記号と呼ぶそうです)
電流制限
LEDの電流について
LEDの光の強度は電流で決まります。
電圧と光の強度は直接は関係していません。
実際は、電圧増加 → 電流増加 → 光量増加のような関係はありますが。
電流で制御するLEDですが、電流が大きすぎると壊れてしまいます。そのため、LEDに流れる電流を制限する必要があります。
すぐに壊れなかったとしても
- 寿命が短くなる
- まぶしすぎて目に優しくない
- 消費電力が上がる
などの懸念があり、あまり推奨されません。
電流を制限する方法は
- LEDドライバIC
- 定電流回路
- 電流制限抵抗 ← この記事で説明します
などがあります。
LEDに流せる最大電流
LEDのデータシートに載っています。
例として秋月電子のサイトで特性が近そうで色が違うLEDをピックアップしてきました。
| 色 | 型番 | 標準電流 | VF | 逆耐圧 |
|---|---|---|---|---|
| 赤 | OSR5JA3Z74A | 30 mA | 2.1 V | 5.0 V |
| 緑 | OSG5TA3Z74A | 30 mA | 3.1 V | 5.0 V |
| 青 | OSB5YU3Z74A | 30 mA | 3.1 V | 5.0 V |
| 白 | OSW4YK3Z72A | 30 mA | 3.1 V | 5.0 V |
どれも標準電流が30 mAとなっているので、実際の回路で使用するときにはLEDを流れる電流が30 mAを超えないようにする必要があります。
表の標準電流という言葉は販売ページに書いてあったものです。
データシートを確認するとAbsolute Maximum RatingのDC Forward Current に30 mAとあるので、最大電流と同義と考えてよさそうです。
VF (順方向電圧降下)
順方向に電流を流すために、LEDにある値以上の電圧(←LED製品ごとに決まっている)をかける必要があります。
これがVFの大きさです。
一般的にLEDのVFは、赤色で2 V前後、青色や白色は3~3.6 V程度です。上の表もそうなっています。
電源の電圧は少なくともVFは必要なので、1.5 Vの乾電池1本ではLEDを点灯させられません。乾電池1本で点灯させるためには昇圧回路が必須となります。
逆耐圧
アノードとカソードを逆につないで電圧をかけたときに耐えられる電圧です。この電圧までなら逆方向に電流は流れません。
逆方向に耐圧以上の電圧をかけると電流が流れ始めます。そしてLEDが壊れます。
制限抵抗 (電流制限抵抗)と計算方法
電流制限抵抗
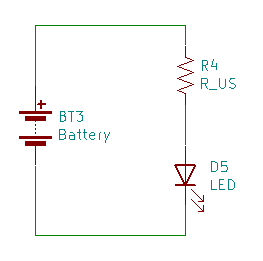
LEDに流れる電流を制限するためにLEDに直列に接続する抵抗が電流制限抵抗です(下の回路図ではR4)。単に制限抵抗ともいいます。
計算に使う法則
オームの法則
抵抗値Rは、「その抵抗にかかる電圧Vを、抵抗を流れる電流Iで割る」と求められます。言い換えると「電圧と電流は比例し、その比例定数が抵抗」でもあります。
\[R = \frac{V}{I}\]
キルヒホッフの第一法則 (電流則)
- 回路全体で、電流は増えたり減ったりしない
- 枝分かれした回路に流れる電流の和は、枝分かれする前の電流と等しい
要するに、さっきの図の回路なら電源(BAT1)と抵抗(R4)とLED(D5)には同じ電流が流れるということです。
キルヒホッフの第二法則 (電圧則)
- 閉じた回路で電圧の方向を一方向に決めたとき、各素子の電圧の和は0
さっきの図でいうと
- 電源(BAT1)の電圧(の和)
- 負荷(R4とD5それぞれ)で降下する電圧の和
が等しいということ。
計算まとめ
オームの法則と、キルヒホッフの法則で計算します。ポイントを整理します。
- キルヒホッフの第一法則より、抵抗とLEDには同じ大きさの電流が流れる
- データシートなどを見てLEDに流す電流を自分で決める (数mAぐらい)
- LEDのVF(順方向電圧降下)特性より、LEDにかかる電圧はVF[V]
- キルヒホッフの第二法則より、抵抗にかかる電圧は「電源電圧-VF」
- 抵抗に流れる電流と抵抗にかかる電圧から、オームの法則で抵抗値を求める
計算例
先ほどの回路を例にして抵抗値を計算してみます。

この後に載せるシミュレーションと同じ条件にします。
- 電源電圧は12 V
- LEDのVFは3.14 V
- LEDに流す電流を5 mA
この条件を満たすための抵抗値を求めてみます。
- LEDと抵抗に流れる電流をIとすると \(I = 0.005\)
- 抵抗にかかる電圧VRとすると \(V_R = V – V_F\)
- 求める抵抗値をRとする
- オームの法則よりRを求める
\[ R = \frac{V_R}{I} = \frac{V-V_f}{I} = \frac{12-3.14}{0.005} = 1772 \]
となって、1772 Ωの抵抗を使うとLEDの電流が5 mAになります。
シミュレーションで確認
LTspiceでざっと確認してみました。適当にピックアップしたNSCW100というLEDに約5 mAを流すための抵抗値を求めました。
LEDのVFはデータシートを見るべきなのですが、今回はシミュレーションから値を拾いました。VF = 3.14 Vとしています。電源電圧は12 Vとしました。
\[R = \frac{12-3.14}{0.005} = 1772\]
となり(さっきと同じ計算ですが)、約1.8 kΩの抵抗を直列に入れればよいということになります。下の画像は1.8 kΩでシミュレーションした結果です。
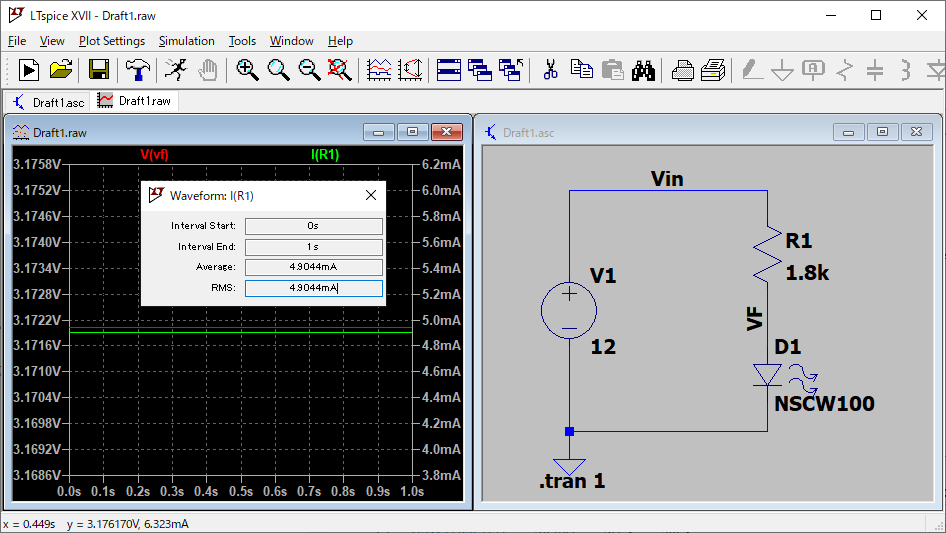
抵抗を流れる電流が4.9 mAとなっていて、求めた抵抗値は正しいことが確認できました。
LEDが複数個あるとき
LEDが複数ある場合の検討は別記事にまとめました。













コメントを残す