新しい記事を書きました。LTspiceを使った電流値の確認も行って、新しい記事を書きました。よろしければそちらもご覧ください。
続きです。
前回はLEDが1個の場合を考えました。引き続いて電源が1つでLEDが複数の場合のつなぎ方と制限抵抗を考えてみます。
目次 1. LED (発光ダイオード) 2. 電流制限 2-1. LEDの電流について 2-2. LEDに流せる最大電流 2-3. VF (順方向電圧降下) 2-4. 逆耐圧 3. 制限抵抗 (電流制限抵抗)と計算方法 3-1. 電流制限抵抗 3-2. 計算に使う法則 3-2-1. オームの法則 3-2-2.
複数個LEDの接続
2個以上のLEDのつなぎ方には直列と並列の2通りがあります。
一概にどちらがいいとは言い切れませんが、以下の考え方を目安にすればいいと思います。
直列接続
LEDのカソードに次のLEDのアノードを接続して数珠つなぎにします。
電流は線路上のどこでも同じ、線路上の電圧は素子を通るたびに下がっていきます。
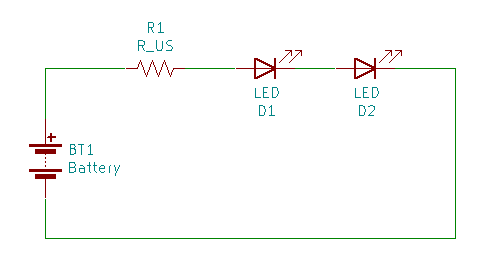
- LED間の光量ばらつきを抑えたいとき
途中で分岐がなく、どのLEDにも同じ電流が流れるため - 抵抗の数を減らしたいとき
電流値を決める必要がある経路が1つなので抵抗が1個(合成抵抗にする場合は2個)でよい
並列接続
(図では)抵抗の片側をまとめて電源の正極に接続、LEDのカソードをまとめて電源の負極に接続します。
分岐後のそれぞれの経路に同じ電圧がかかります。
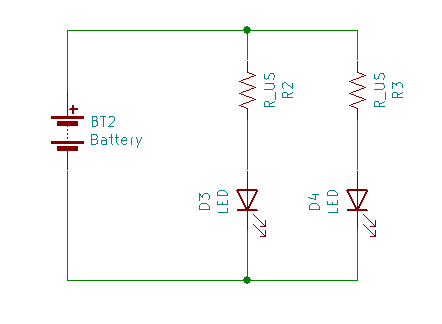
- 電源電圧がVFに対してあまり高くないとき
直列に接続すると負荷での電圧降下がVFの足し合わせになるので駆動できない
制限抵抗値の計算
直列接続
制限抵抗は1個です。LEDのVFの合計と電源電圧との差が抵抗にかかる電圧です。この抵抗にかかる電圧とLEDと抵抗を流れる電流からオームの法則で抵抗値を求めます。

条件は前回のLEDが1個のときと同じとして、制限抵抗の値を求めてみます。
- 電源電圧は12 V
- LEDのVFは3.14 V
- LEDに流す電流を5 mA
- LEDと抵抗に流れる電流をIとすると \(I = 0.005\)
- 抵抗にかかる電圧VRとすると \(V_R = V – V_F *2\)
- 求める抵抗値をRとする
- オームの法則よりRを求める
\[ R = \frac{V_R}{I} = \frac{V-V_F *2}{I} = \frac{12-3.14*2}{0.005} = 1144 \]
となって、R1に1144 Ωの抵抗を使うとLEDの電流が5 mAになります。
並列接続
LEDが2個の下図の回路を考えます。LEDが2個なので抵抗も2個必要です。
分岐後の経路ごとに考えるとLEDが1個なので、今までと同様に電源電圧とVFの差をとってからオームの法則で抵抗値を求めることができます。それぞれの抵抗+LEDにかかる電圧は電源電圧と同じです。

今回は2つのLEDのVFが異なるとして計算してみます。
- 電源電圧は12 V
- LEDのVFはD3(左)が2 V、D4(右)が3.6 V
- 各LEDに流す電流を5 mA
左(D3)の経路
- LEDと抵抗に流れる電流をILとすると \(I_L = 0.005\)
- 抵抗にかかる電圧VRLとすると \(V_{RL} = V – V_{F3}\)
- 求める抵抗値をRLとする
- オームの法則よりRLを求める
\[ R_L = \frac{V_{RL}}{I_L} = \frac{V-V_{F3}}{I_L} = \frac{12 – 2}{0.005} = 2000 \]
となり、R2に2000 Ωの抵抗を使うとLEDの電流が5 mAになります。
右(D4)の経路
同様に
- LEDと抵抗に流れる電流をIRとすると \(I_R = 0.005\)
- 抵抗にかかる電圧VRRとすると \(V_{RR} = V – V_{F4}\)
- 求める抵抗値をRRとする
- オームの法則よりRRを求める
\[ R_R = \frac{V_{RR}}{I_R} = \frac{V – V_{F4}}{I_R} = \frac{12 – 3.6}{0.005} = 1680 \]
となり、R3は1680 Ωの抵抗にすると電流が5 mAになります。
まとめ
接続方法
LEDを複数個駆動するときは接続方法が2つある。
- 直列はこんなとき
- LED間の光量ばらつきを抑えたいとき
- 抵抗の数を減らしたいとき
- 並列はこんなとき
- 電源電圧がVFに対してあまり高くないとき
計算方法
制限抵抗を求める計算は次のように。
- 直列ではVFの足し合わせを使う
- 並列では経路ごとに計算する













コメントを残す